Monte-Carlo Simulation in Derivative Pricing
Financial instruments are monetary contracts between parties. They can be created, traded, modified and settled. They can be cash (currency), evidence of an ownership interest in an entity (share), or a contractual right to receive or deliver cash (bond).
One specialized type of the above is called a Note. A note is a debt security obligating repayment of a loan at a dynamic interest rate in a defined time period. The interest rate is determined by complex rules whose outputs depend on future market values that cannot be accurately predicted.
In the real world, when millions are at stake, it becomes an utmost priority to make sure that the note a company selects for investing has minimal risk. One of our flagship products, Derivator has a sub feature that specializes to solve this problem.
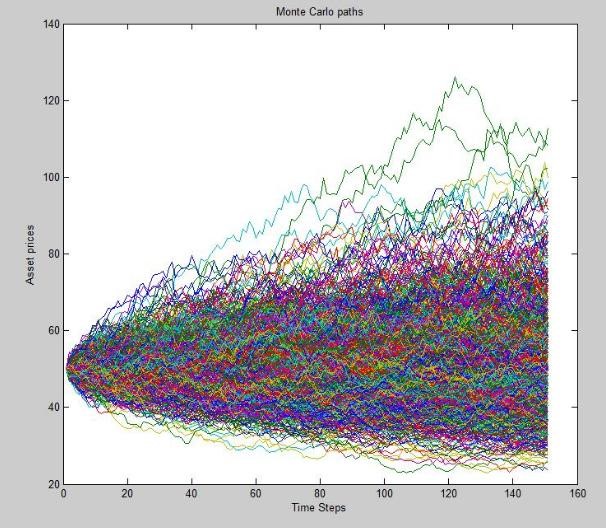
The process starts off with carefully analyzing the note with the help of a human to make sure that the minute details of the note such as observation and redemption dates, complex rules and custom needs of the user are taken care off. The data is then passed on to out model which takes in the probability of each variable that cannot be determined, for example, the stock value of the issuing company 4 years from now.
The model is then run thousands of times to simulate various future market scenarios and determines an accurate value of the return on investment. It uses several methods such as Heston, Hull White and SABR models. These methods are widely used in the financial industry and have been proven from time to time.
One important concept – Stochastic volatility refers to the fact that the volatility of asset prices is not constant, as assumed in the Black Scholes options pricing model. The word “stochastic” refers to something that is randomly determined and may not be predicted precisely. Stochastic volatility modeling attempts to correct for this problem with Black Scholes by allowing volatility to vary over time.
Examples of stochastic volatility models include the Heston model and the SABR model. Both of the above models have been implemented in our product.
These models use statistical methods to calculate and forecast option pricing with the assumption that volatility is arbitrary. The assumption that volatility is arbitrary rather than constant is the key factor that makes stochastic volatility models unique. Combining all these 3 models instead of just 1 considering their unique shortcomings and strength is what makes our product unique.
Running the same note on multiple models as mentioned above makes sure that the ROI value outputted by our product is accurate. This way your company can assess the risk that comes with the investment accurately and thus take smart decisions.
Follow