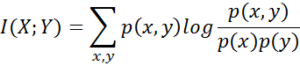Concepts of Information theory

Information theory is a very important field of study having significant impact on modern data science and analytics space. Some of the fundamental concepts of information theory also form the base for many machine learning models. So before we dig deep into concepts of information theory, let’s see what information theory is.
Information theory studies the transmission, processing, extraction, and utilization of information. Given a set of random variables, what can we say about information content in them? This is the central problem in information theory. The field is at the intersection of mathematics, statistics, computer science and concepts from physics. The application of information can be found in many data science problems like Natural Language Processing, Data Mining and Machine Learning.

There are two fundamental concepts of information theory widely applicable in analytics. Those are Entropy and Mutual Information.

Entropy

Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Entropy is calculated using following formula.
Entropy is a non-negative number. It is zero when the random variable is “certain”.

Conditional entropy quantifies the amount of information needed to describe the outcome of a random variable Y given that the value of another random variable X is known.
In a simple terms, when you have two random variables and want know whether one can be inferred or predicted if the other one is known, conditional entropy can come to rescue. Like entropy, conditional entropy is non-negative as well. It is zero if one variable can be predicted certainly if other is known. Following is the equation for calculating conditional entropy.

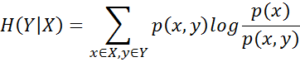
Mutual information is a measure of the mutual dependence between the two variables. It is one of many quantities that measures how much one random variables tells us about another. It is a dimensionless quantity with units of bits, and can be thought of as the reduction in uncertainty about one random variable given knowledge of another. High mutual information indicates a large reduction in uncertainty; low mutual information indicates a small reduction; and zero mutual information between two random variables means the variables are independent.
Mutual Information is a measure of association between two variables unlike entropy which is a measure of uncertainty. Following is the equation of calculating MI.

Point-wise mutual information is similar to mutual information, but it refers to a single event whereas mutual information is the average of all possible events. For a simplicity consider PMI as an intermediate step of calculating MI. Following equation of PMI will make it clearer if you compare it with the equation of MI.

We rigorously make use of above concepts of information theory in our flagship product Narrator. We use these methods to find the association of variables with each other and identify the significant insights.
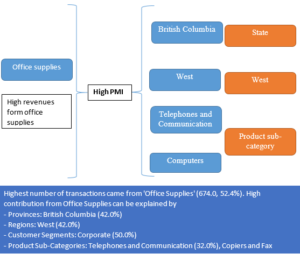
Narrator has a module called automated analysis where it shows various analyses and insights on its own without any manual intervention. One of those analysis is multi-level analysis where we show the analysis of 2 variables and relevant insights. Here we use conditional entropy to identify whether a variable is perfectly dependent on another variable and treat that insight differently. We also make use of mutual information to see whether the 2 variable have any kind of relationship between them. If there is no relationship, then that analysis will not be displayed in automated analysis section.

Narrator gives very interesting insights about your data including the causality. For e.g. if your maximum sales has come from a particular product, then it will tell you what all could be the possible reasons behind it or what factors have contributed to more sales for that particular product category.
Information theory gives powerful tools to identify insights and patterns from data, which are not easily identifiable with other statistical analyses.